Manuel D. Barriga-Carrasco, Universidad de Castilla-La Mancha
Como se sabe, los postulados de Einstein nos obligan a redefinir ciertos conceptos de la física clásica, como la masa y la energía. Tomemos, por ejemplo, la nueva masa relativista que se mueve a velocidades próximas a la de la luz. No tiene un valor constante, sino que varía según su velocidad. Sin embargo, a velocidades pequeñas –comparadas con las de la luz–, se comporta como la masa clásica y vuelve a tener un valor constante.
Esta masa relativista también tiene que seguir los postulados de Einstein: no puede adquirir una velocidad más grande que la de la luz. Para ello se tiene que hacer muy grande, infinita, cuando su velocidad se acerca a la de la luz. Al hacerse infinita la masa, ninguna fuerza finita podrá acelerarla para superar la velocidad de la luz.
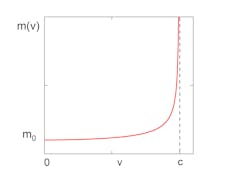 Cómo aumenta la masa relativista (m) conforme su velocidad se acerca a la de la luz (c)
Cómo aumenta la masa relativista (m) conforme su velocidad se acerca a la de la luz (c)
Pero, ¿cuál es la energía cinética de una partícula relativista? ¿La misma que la clásica, considerando la masa relativista? No es tan sencillo.
Como dijimos en el artículo anterior, los postulados de Einstein nos llevan a redefinir los conceptos clásicos, como masa y energía, pero se mantienen los principios y leyes de la física.
Calcularemos la energía cinética relativista, Ek, a partir de la definición clásica de la energía cinética, que nos dice que es la ganancia de energía de la partícula debida al trabajo hecho por una fuerza externa que produce un cambio en su velocidad, esto es conocido como “teorema de las fuerzas vivas”. El resultado nos da:
Ek = mc² - m₀c²
Esta fórmula nos recuerda a la famosa relación de Einstein. Aquí m es la masa relativista, c la velocidad de la luz, y m₀ es esa masa constante de la que hablábamos antes, llamada masa en reposo, porque es la que tiene la partícula cuando su velocidad se hace cero (o muy pequeña comparada con la de la luz como en física clásica).
Si observamos otra vez la fórmula, vemos que cuando la velocidad se haga cero, la masa relativista será igual a la masa en reposo y por tanto la energía cinética será cero, lo cual era de esperar. La cantidad constante E₀ = m₀ c² , tiene unidades de energía y por eso se le llama energía en reposo, que es la energía que toda partícula tiene por el hecho de tener masa en reposo. Para velocidades próximas a la velocidad de la luz, la energía cinética relativista se hace infinita al igual que la masa relativista.
La energía total relativista de una partícula será la suma de la energía cinética, debido a que se está moviendo, más la energía en reposo obteniendo,
E = mc²
Esta sí que es la famosa relación de Einstein. Esta expresión indica que la masa y la energía relativistas son equivalentes, ya que simplemente están multiplicadas por una constante c². Esto significa que una ganancia en masa relativista sería equivalente a una ganancia en energía y viceversa.
El fin de nuestro sol
Para entender mejor esto, podemos poner un ejemplo sencillo. Vamos a suponer que la energía luminosa que nos da una bombilla incandescente proviene de la masa de su filamento. Gracias a la fórmula de Einstein podríamos estimar qué pérdida de masa tiene este filamento cuando esta bombilla ha estado funcionando, por ejemplo, un año entero.
Si la bombilla es de 100 vatios, la energía emitida (y por tanto perdida por la bombilla) durante un año es 3.15x10⁹ julios, que dividida por la velocidad de la luz al cuadrado nos da una pérdida de masa del filamento de 3.5x10⁻⁸ kilogramos. ¡Esta podría ser una buena estimación de la masa que pierde un filamento de una bombilla incandescente en un año!
De la misma manera, podríamos estimar el tiempo que va a vivir nuestro Sol.
Podemos establecer un símil entre la bombilla incandescente y el astro rey. Si conocemos la energía que emite el Sol, según la relación de Einstein podemos calcular su pérdida de masa. Si perdiera toda su masa, ese sería su fin.
Se sabe que la potencia del Sol es aproximadamente de unos 4x10²⁶ vatios y su masa de unos 2x10³⁰ kilogramos. Por tanto, multiplicando su masa por la velocidad de la luz al cuadrado tendremos su masa convertida en energía, que por la conservación de la masa y energía es el máximo de energía que podría emitir.
Si pensamos que la potencia del Sol es constante, el tiempo que tardaría en emitir toda esa energía sería el tiempo de vida máximo de nuestro Sol. Es decir, si dividimos esa energía por la potencia que tiene nuestro Sol obtenemos su tiempo de vida máximo, que es igual a unos 1.42x10¹³ años. ¡Podemos dormir tranquilos!
Manuel D. Barriga-Carrasco, Profesor del Área de Mecánica de Fluidos de la Escuela Técnica Superior de Ingenieros Industriales, Universidad de Castilla-La Mancha
Este artículo fue publicado originalmente en The Conversation. Lea el original.